Creating and Exercising a Custom Single Degree of Freedom System

Note

You can download this example as a Python script: custom-sdof-system.py or Jupyter notebook: custom-sdof-system.ipynb.

Creating a new system

The first step is to import a “blank” SingleDoFLinearSystem and initialize it.

from resonance.linear_systems import SingleDoFLinearSystem

msd_sys = SingleDoFLinearSystem()

Now define the constant variables for the system. In this case, the single degree of freedom system will be described by its mass, natural frequency, and damping ratio.

msd_sys.constants['m'] = 1.0  # kg
msd_sys.constants['fn'] = 1.0  # Hz
msd_sys.constants['zeta'] = 0.1  # unitless

msd_sys.constants

{'m': 1.0, 'fn': 1.0, 'zeta': 0.1}

Define the coordinate and speed. The software assumes that the speed is defined as the time derivative of the coordinate, i.e. \(v = \dot{x}\).

msd_sys.coordinates['x'] = 1.0  # m
msd_sys.speeds['v'] = 0.0  # m/s

msd_sys.coordinates

{'x': 1.0}

msd_sys.speeds

{'v': 0.0}

msd_sys.states

{'x': 1.0, 'v': 0.0}

Now that the coordinate, speed, and constants are defined the equations of motion can be defined. For a single degree of freedom system a Python function must be defined that uses the system’s constants to compute the coefficients to the canonical second order equation, \(m \dot{v} + c v + k x = 0\).

The inputs to the function are the constants. The variable names should match those defined above on the system.

import numpy as np

def calculate_canonical_coefficients(m, fn, zeta):
    """Returns the system's mass, damping, and stiffness coefficients given
    the system's constants."""
    wn = 2*np.pi*fn
    k = m*wn**2
    c = zeta*2*wn*m
    return m, c, k

msd_sys.canonical_coeffs_func = calculate_canonical_coefficients

Once this function is defined and added to the system \(m,c,k\) can be computed using:

msd_sys.canonical_coefficients()

(1.0, 1.2566370614359172, 39.47841760435743)

The period of the natural frequency can be computed with:

msd_sys.period()

1.005037815259212

All information about the system can be displayed:

msd_sys

System name: SingleDoFLinearSystem

Canonical coefficients function defined: True
Configuration plot function defined: False
Configuration update function defined: False

Constants
=========
m = 1.00000
fn = 1.00000
zeta = 0.10000

Coordinates
===========
x = 1.00000

Speeds
======
v = d(x)/dt = 0.00000

Measurements
============

Simulating the free response

The free_response() function simulates the now fully defined system given as an initial value problem. One or both of the coordinates and speeds must be set to provide a free response. The following shows the response to both \(x\) and \(v\) being set to some initial values.

msd_sys.coordinates['x'] = -5.0
msd_sys.speeds['v'] = 8.0

free_response() returns a Pandas DataFrame with the time values as the index and columns for the coordinate, speed, and additionally the time derivative of the speed (acceleration in this case). See https://pandas.pydata.org/pandas-docs/stable/getting_started/dsintro.html for an introduction to DataFrame.

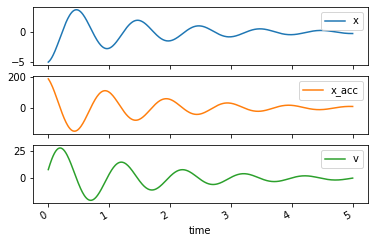
trajectories = msd_sys.free_response(5.0)
trajectories
x x_acc v
time
0.00 -5.000000 187.338992 8.000000
0.01 -4.910728 181.496514 9.844723
0.02 -4.803311 175.015195 11.627801
0.03 -4.678398 167.928429 13.343009
0.04 -4.536697 160.271570 14.984469
... ... ... ...
4.96 -0.217071 8.839775 -0.214970
4.97 -0.218780 8.796369 -0.126761
4.98 -0.219609 8.719006 -0.039156
4.99 -0.219566 8.608415 0.047509
5.00 -0.218663 8.465444 0.132905

501 rows × 3 columns

There are a variety of plotting methods associated with the DataFrame that can be used to quickly plot the trajectories of the coordinate, speed, and acceleration. See more about plotting DataFrames at https://pandas.pydata.org/pandas-docs/stable/user_guide/visualization.html.

axes = trajectories.plot(subplots=True)
_images/custom-sdof-system_12_0.png

Response to change in constants

This system is parameterized by its mass, natural frequency, and damping ratio. It can be useful to plot the trajectories of position for different values of \(\zeta\) for example.

Set the initial conditions back to simply stretching the spring 1 meter:

msd_sys.coordinates['x'] = 1.0
msd_sys.speeds['v'] = 0.0

Now change \(\zeta\) to different values and simulate the free response to see the different damping regimes:

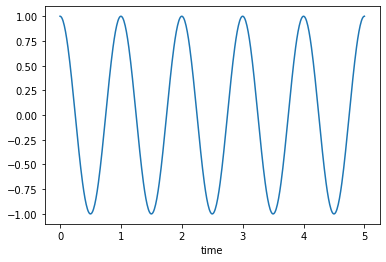
Un-damped, \(\zeta=0\)

msd_sys.constants['zeta'] = 0.0  # Unitless
trajectories = msd_sys.free_response(5.0)
axes = trajectories['x'].plot()
_images/custom-sdof-system_14_0.png

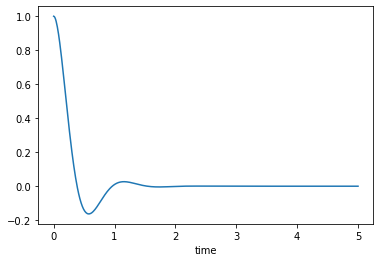
Under-damped, \(0<\zeta<1\)

msd_sys.constants['zeta'] = 0.5  # Unitless
trajectories = msd_sys.free_response(5.0)
axes = trajectories['x'].plot()
_images/custom-sdof-system_15_0.png

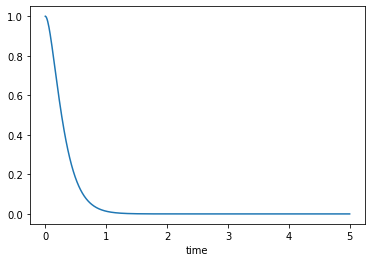
Critically damped, \(\zeta=1\)

msd_sys.constants['zeta'] = 1.0  # Unitless
trajectories = msd_sys.free_response(5.0)
axes = trajectories['x'].plot()
_images/custom-sdof-system_16_0.png

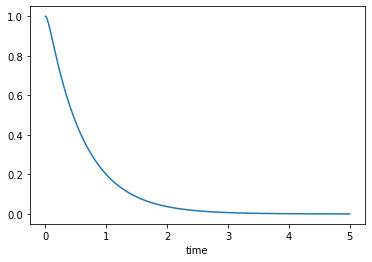
Over-damped, \(\zeta>1\)

msd_sys.constants['zeta'] = 2.0  # Unitless
trajectories = msd_sys.free_response(5.0)
axes = trajectories['x'].plot()
_images/custom-sdof-system_17_0.png

Adding measurements

It is often useful to calculate the trajectories of other quantities. Systems in resonance allow “measurements” to be defined. These measurements are functions of the constants, coordinates, speeds, and/or time. To create a new measurement, create a function that returns the quantity of interest. Here a measurement function is defined that calculates the kinetic energy (\(\frac{1}{2}mv^2\)) of the system and then added to the system with variable name KE.

def calculate_kinetic_energy(m, v):
   return m*v**2/2

msd_sys.add_measurement('KE', calculate_kinetic_energy)

Once added, the measurement will be computed and added to the DataFrame containing the trajectories:

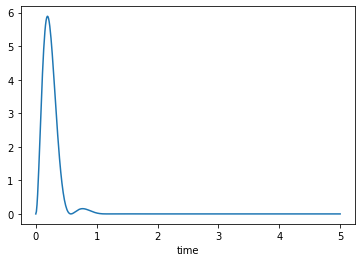
msd_sys.constants['zeta'] = 0.5  # Unitless
trajectories = msd_sys.free_response(5.0)
trajectories
x x_acc v KE
time
0.00 1.000000e+00 -39.478418 8.881784e-16 3.944305e-31
0.01 9.980674e-01 -36.999522 -3.823857e-01 7.310941e-02
0.02 9.924348e-01 -34.530060 -7.400220e-01 2.738162e-01
0.03 9.833490e-01 -32.078904 -1.073048e+00 5.757160e-01
0.04 9.710551e-01 -29.654314 -1.381689e+00 9.545318e-01
... ... ... ... ...
4.96 4.648115e-08 0.000006 -1.189485e-06 7.074377e-13
4.97 3.487003e-08 0.000006 -1.132570e-06 6.413573e-13
4.98 2.383263e-08 0.000006 -1.074788e-06 5.775850e-13
4.99 1.337624e-08 0.000006 -1.016414e-06 5.165491e-13
5.00 3.505453e-09 0.000006 -9.577074e-07 4.586018e-13

501 rows × 4 columns

and can be plotted like any other column:

axes = trajectories['KE'].plot()
_images/custom-sdof-system_20_0.png

Plotting the configuration

resonance systems can plot and animate at the system’s configuration. To do so, a custom function that generates a configuration plot using matplotlib must be defined and associated with the system. Below a plot is created to show an orange block representing the mass and a spring attached to the block. The spring() function conveniently provides the x and y data needed to plot the spring.

import matplotlib.pyplot as plt
from resonance.functions import spring

# create a new constant to describe the block's dimension, l
msd_sys.constants['l'] = 0.2  # m

def create_configuration_figure(x, l):

    # create a figure with one or more axes
    fig, ax = plt.subplots()

    # the `spring()` function creates the x and y data for plotting a simple
    # spring
    spring_x_data, spring_y_data = spring(0.0, x, l/2, l/2, l/8, n=3)
    lines = ax.plot(spring_x_data, spring_y_data, color='purple')
    spring_line = lines[0]

    # add a square that represents the mass
    square = plt.Rectangle((x, 0.0), width=l, height=l, color='orange')
    ax.add_patch(square)

    # add a vertical line representing the spring's attachment point
    ax.axvline(0.0, linewidth=4.0, color='black')

    # set axis limits and aspect ratio such that the entire motion will appear
    ax.set_ylim((-l/2, 3*l/2))
    ax.set_xlim((-np.abs(x) - l, np.abs(x) + l))
    ax.set_aspect('equal')

    ax.set_xlabel('$x$ [m]')
    ax.set_ylabel('$y$ [m]')

    # this function must return the figure as the first item
    # but you also may return any number of objects that you'd like to have
    # access to modify, e.g. for an animation update

    return fig, ax, spring_line, square

# associate the function with the system
msd_sys.config_plot_func = create_configuration_figure

Now the configuration plot can be generated with plot_configuration(). This returns the same results as the function defined above.

fig, ax, spring_line, square = msd_sys.plot_configuration()
_images/custom-sdof-system_22_0.png

Animating the configuration

Reset to un-damped motion and simulate again

msd_sys.constants['zeta'] = 0.1
trajectories = msd_sys.free_response(5.0)

To animate the configuration, create a function that updates the various matplotlib objects using any constants, coordinates, speeds, and/or the special variable time. The last input arguments to this function must be all of the extra outputs of plot_configuration() (excluding the figure which is the first output). The order of these must match the order of the plot_configuration() outputs.

def update_configuration(x, l, time,  # any variables you need for updating
                         ax, spring_line, square):  # returned items from plot_configuration() in same order

    ax.set_title('{:1.2f} [s]'.format(time))

    xs, ys = spring(0.0, x, l/2, l/2, l/8, n=3)
    spring_line.set_data(xs, ys)

    square.set_xy((x, 0.0))

msd_sys.config_plot_update_func = update_configuration

Now that the update function is associated, animate_configuration() will create the animation. Here the frames-per-second are set to an explicit value.

animation = msd_sys.animate_configuration(fps=30)
_images/custom-sdof-system_25_0.png

If using the notebook interactively with %matplotlib widget set, the animation above will play. But animate_configuration() returns a matplotlib FuncAnimation object which has other options that allow the generation of different formats, see https://matplotlib.org/api/_as_gen/matplotlib.animation.FuncAnimation.html for options. One option is to create a Javascript/HTML versions that displays nicely in the notebook with different play options:

from IPython.display import HTML

HTML(animation.to_jshtml(fps=30))

Response to sinusoidal forcing

The response to a sinusoidal forcing input, i.e.:

\[m\dot{v} + cv + kx = F_o \sin(\omega t)\]

can be simulated with sinusoidal_forcing_response(). This works the same as free_response except it requires a forcing amplitude and frequency.

msd_sys.coordinates['x'] = 0.0  # m
msd_sys.speeds['v'] = 0.0  # m/s

Fo = 10.0
omega = 2*np.pi*3.0  # rad/s

forced_trajectory = msd_sys.sinusoidal_forcing_response(Fo, omega, 5.0)

Note that there is now a forcing_function column. This is the applied forcing function.

forced_trajectory
x x_acc v KE forcing_function
time
0.00 0.000000 10.000000 6.938894e-18 2.407412e-35 10.000000
0.01 0.000496 9.679225 9.871978e-02 4.872797e-03 9.822873
0.02 0.001957 8.978820 1.923176e-01 1.849302e-02 9.297765
0.03 0.004313 7.924765 2.771159e-01 3.839662e-02 8.443279
0.04 0.007459 6.555691 3.497615e-01 6.116656e-02 7.289686
... ... ... ... ... ...
4.96 -0.023218 8.674053 -3.722232e-01 6.927505e-02 7.289686
4.97 -0.026486 9.839976 -2.793765e-01 3.902562e-02 8.443279
4.98 -0.028773 10.655573 -1.765928e-01 1.559251e-02 9.297765
4.99 -0.029997 11.091961 -6.753058e-02 2.280189e-03 9.822873
5.00 -0.030115 11.133696 4.392935e-02 9.648938e-04 10.000000

501 rows × 5 columns

The trajectories can be plotted and animated as above:

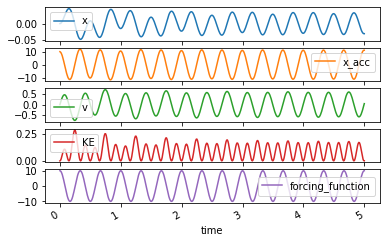
axes = forced_trajectory.plot(subplots=True)
_images/custom-sdof-system_29_0.png 
fps = 30
animation = msd_sys.animate_configuration(fps=fps)
_images/custom-sdof-system_30_0.png 
HTML(animation.to_jshtml(fps=fps))

Frequency response

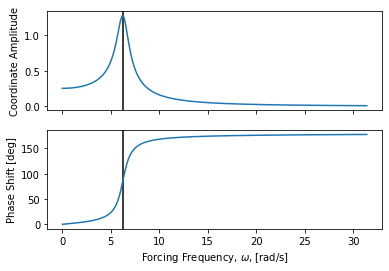
The frequency response to sinusoidal forcing at different frequencies can be plotted with frequency_response_plot() for a specific forcing amplitude.

axes = msd_sys.frequency_response_plot(Fo)
_images/custom-sdof-system_32_0.png

Response to periodic forcing

Any periodic forcing function can be applied given the Fourier series coefficients of the approximating function. The following function calculates the Fourier series coefficients for a “sawtooth” shaped periodic input.

def sawtooth_fourier_coeffs(A, N):
    """
    A : sawtooth amplitude, Newtons
    T : sawtooth period, seconds
    N : number of Fourier series terms
    """
    n = np.arange(1, N+1)
    an = A*(8*(-1)**n - 8) / 2 / np.pi**2 / n**2
    return 0, an, np.zeros_like(an)

a0, an, bn = sawtooth_fourier_coeffs(Fo, 20)

These coefficients can be provided to periodic_forcing_response() to simulate the response:

wb = 2*np.pi*3.0  # rad/s

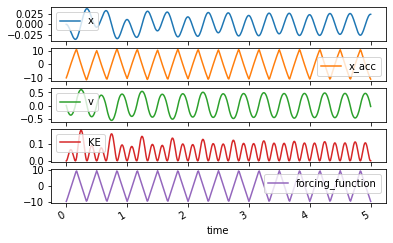
trajectory = msd_sys.periodic_forcing_response(a0, an, bn, wb, 5.0)
trajectory
x x_acc v KE forcing_function
time
0.00 -3.469447e-18 -9.797526 -6.938894e-18 2.407412e-35 -9.797526
0.01 -4.773325e-04 -8.653652 -9.344627e-02 4.366102e-03 -8.789924
0.02 -1.821290e-03 -7.332725 -1.731808e-01 1.499579e-02 -7.622252
0.03 -3.896544e-03 -5.927083 -2.395012e-01 2.868041e-02 -6.381879
0.04 -6.565825e-03 -4.583400 -2.921305e-01 4.267012e-02 -5.209711
... ... ... ... ... ...
4.96 1.860597e-02 -6.335998 3.117475e-01 4.859327e-02 -5.209711
4.97 2.138612e-02 -7.530659 2.423054e-01 2.935596e-02 -6.381879
4.98 2.341220e-02 -8.748665 1.608547e-01 1.293711e-02 -7.622252
4.99 2.456569e-02 -9.845257 6.805327e-02 2.315623e-03 -8.789924
5.00 2.473372e-02 -10.728694 -3.603302e-02 6.491893e-04 -9.797526

501 rows × 5 columns

axes = trajectory.plot(subplots=True)
_images/custom-sdof-system_35_0.png 
fps = 30
animation = msd_sys.animate_configuration(fps=fps)
_images/custom-sdof-system_36_0.png 
HTML(animation.to_jshtml(fps=fps))